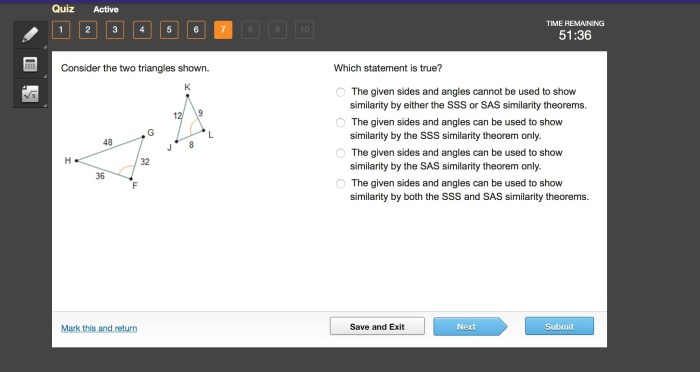
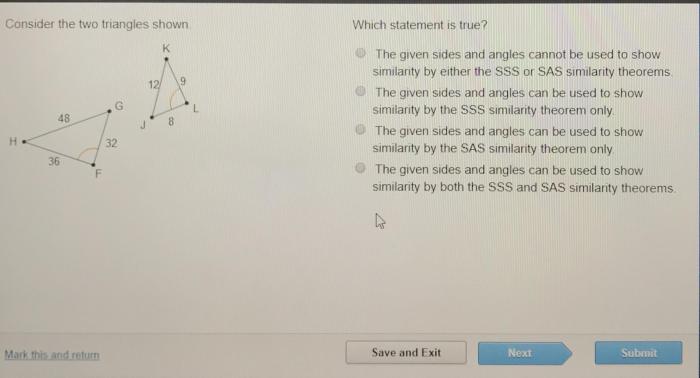
Consider the two triangles shown. Which statement is true? This question delves into the realm of triangle congruence, a fundamental concept in geometry. By examining the properties and relationships between triangles, we can determine whether they are congruent and explore the implications of this congruence.
Triangle congruence theorems, such as SSS, SAS, ASA, and AAS, provide the foundation for determining triangle congruence. These theorems establish criteria based on side lengths and angles that, when satisfied, guarantee the congruence of triangles. Understanding these theorems is crucial for analyzing and solving problems involving triangles.
Triangle Congruence Theorems
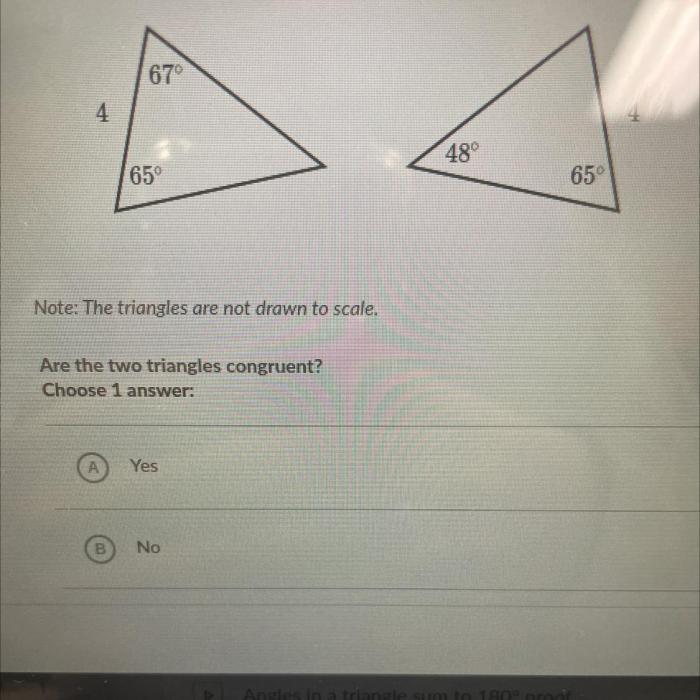
Triangle congruence theorems are a set of rules that can be used to determine if two triangles are congruent. The three main triangle congruence theorems are:
- Side-Side-Side (SSS) Theorem: If the three sides of one triangle are congruent to the three sides of another triangle, then the two triangles are congruent.
- Side-Angle-Side (SAS) Theorem: If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent.
- Angle-Side-Angle (ASA) Theorem: If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent.
Triangle Properties
Triangles have a number of properties that can be used to analyze them. Some of the most important properties include:
- The sum of the interior angles of a triangle is 180 degrees.
- The sum of the exterior angles of a triangle is 360 degrees.
- The longest side of a triangle is opposite the largest angle.
- The shortest side of a triangle is opposite the smallest angle.
Triangle Relationships
There are a number of different types of triangles, including equilateral triangles, isosceles triangles, and scalene triangles.
- Equilateral triangles have three congruent sides.
- Isosceles triangles have two congruent sides.
- Scalene triangles have no congruent sides.
Triangle Inequality Theorem
The triangle inequality theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
Coordinate Geometry
Coordinate geometry can be used to analyze triangles. The coordinates of the vertices of a triangle can be used to determine the length of the sides of the triangle, the area of the triangle, and the perimeter of the triangle.
Applications of Triangles, Consider the two triangles shown. which statement is true
Triangles are used in a variety of real-world applications, including architecture, engineering, and navigation.
- In architecture, triangles are used to create strong and stable structures.
- In engineering, triangles are used to design bridges, airplanes, and other structures.
- In navigation, triangles are used to determine the location of a ship or airplane.
Expert Answers: Consider The Two Triangles Shown. Which Statement Is True
What is the Triangle Congruence Theorem?
The Triangle Congruence Theorem states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent.
What are the different types of triangles?
Triangles can be classified into three types based on their side lengths: equilateral (all sides equal), isosceles (two sides equal), and scalene (no sides equal).
How can I use coordinate geometry to analyze triangles?
Coordinate geometry allows you to represent triangles on a coordinate plane and use algebraic equations to determine their properties, such as area, perimeter, and centroid.